Let's rewrite the equation:
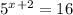
To answer this question, we can start by applying log in both sides. We can choose the base of the log, let's use base 10, which is the most common one:
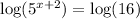
Now we use a the following property of log:
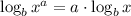
So:
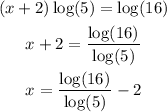
We can use a calculator to get the log(16) and log(5). Alternatively, we can use a table of log base 10 values. We get:

So, the value of x to the nearest thousandths is -0.277.