Question

Match the exponential graphs to the situations below in which the investments lose money

Answer 1

For exponential functions, they are defined by the general formula:

`f(x)=ab^x`

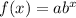
From the graph given in the question, we can deduce that

when

`\begin{gathered} x=0,y=200 \\ x=1,y=180 \end{gathered}`

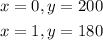
With this, we can derive the values of a and b

so that

`\begin{gathered} 200=a* b^0 \\ 200=a \end{gathered}`

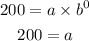
Similarly, we can get b by substituting the value of a=200 and y=180 when x=1 into the equation

`\begin{gathered} 180=200* b^1 \\ b=(180)/(200)=0.9 \end{gathered}`

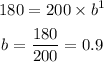
Thus the formula is

`y=200(0.9)^x`

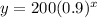
The 0.9 means that there is a loss of 10% every year

Therefore

The correct answer is

$200 at a 10% loss per year