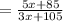Question

Simplify the complex fraction, rewriting it by multiplying the numerator and denominator by the LCD

Answer 1

Given the complex fraction:

`((1)/(3)+(4)/(x+5))/((6)/(x+5)+(1)/(5))`

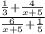
You can simplify it as follows:

1. Find the LCD (Least Common Denominator). In this case:

`LCD=(3)(5)(x+5)=15(x+5)`

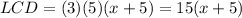
2. Multiply the numerator and the denominator of the complex fraction by the LCD, in order to get rid of the denominators of the fractions that form the complex fraction:

`=(((1)/(3))\lbrack15(x+5)\rbrack+((4)/(x+5))\lbrack15(x+5)\rbrack)/(((6)/(x+5))\lbrack15(x+5)\rbrack+((1)/(5))\lbrack15(x+5)\rbrack)`

Notice that you can simplify multiply and simplify as follows (you can see below the process for simplifying each fraction that forms the complex fraction):

`((1)/(3))\lbrack15(x+5)\rbrack=(\lbrack15(x+5)\rbrack)/(3)=5(x+5)`
`((4)/(x+5))\lbrack15(x+5)\rbrack=(4\lbrack15(x+5)\rbrack)/(x+5)=(60(x+5))/(x+5)=60`
`((6)/(x+5))\lbrack15(x+5)\rbrack=(6\lbrack15(x+5)\rbrack)/(x+5)=(90(x+5))/(x+5)=90`
`((1)/(5))\lbrack15(x+5)\rbrack=(\lbrack15(x+5)\rbrack)/(5)=3(x+5)`

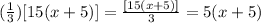
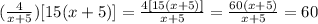
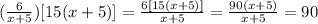
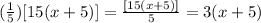
Then, you can rewrite the expression as follows:

`=(5(x+5)+60)/(90+3(x+5))`

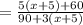
3. Apply the Distributive Property in the numerator and in the denominator:

`=((5)(x)+(5)(5)+(60))/(90+(3)(x)+(3)(5))`
`=(5x+25+60)/(90+3x+15)`

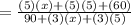
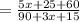
4. Add the like terms in the numerator and in the denominator:

`=(5x+85)/(3x+105)`

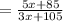
Hence, the answer is:

`=(5x+85)/(3x+105)`