How to transform into an expression with a rational exponent

Question

asked May 12, 2023 142k views

1 Answer

Konstantin Weitz · Answer 1 · 2023-05-17T21:36:49+0000

Given the expression:

$(\sqrt[6]{x^5})^7$

Let's transform the expression into an expression with rational exponents.

To transform into an expression with rational exponents, apply the formula:

$\sqrt[n]{a^x}=a^{(x)/(n)}$

Thus, we have:

$(\sqrt[6]{x^5})^7=(x^{(5)/(6)})^7$

Now, apply the power rule and multiply the exponents:

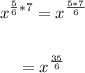
$\begin{gathered} x^{(5)/(6)*7}=x^{(5*7)/(6)} \\ \\ =x^{(35)/(6)} \end{gathered}$

Therefore, the expression written with rational exponents is:

$x^{(35)/(6)}$

ANSWER:

$x^{(35)/(6)}$