Notice that in this case, you are given the measure of the three sides of a triangle. In such conditions, the appropriate Law to use is the Law of Cosines. ANd also, since they want you to find the SMALLEST angle, have in mind that the smallest angle always opposes the shortes side in a triangle.
Then we want to use the Law of Cosines:
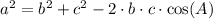
So we use the smalles side (in our case b = 11) to write the appropriate Law of cosines as shown below:
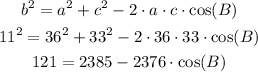
And we solve for cos(B) as follows:
cos(B) = (121-2385) / (-2376) = 0.95286
Now we use arccos to find the angle:
< B = arccos(0.95286) = 17.66 degrees
So we select the answer labeled C that shows the rounding of this value to one decimal:
17.7 degrees.