Answer:
m=12
Explanation:
Given any quadratic function, y=ax²+bx+c.
We can determine the nature of the roots of such quadratic function by examining the discriminant, D where:
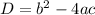
• If D>0, the roots are real and unequal.
,
• If D=0, the roots are real and equal.
,
• If D<0, the roots are complex.
In our given equation:
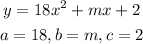
For the function to have exactly one zero, the value of D=0.

The value of m for which the function will have one zero is 12.