The piecewise function for the cost of the ad "c" that depends on the number of lines "x" is:
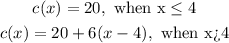
The first piece of the function is useful to calculate the cost of 1, 2, 3, or 4 lines. Remember that "x" is the number of lines.
But since we need to calculate the cost of 5 lines, we are going to need the second piece of the function:
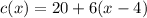
Because the condition to use it is that x is greater than 4, and since 5 is greater than 4, we can use it.
Thus, substitute x=5 into the function:

And solve the operations. First, solve the subtraction inside the parenthesis:
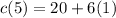
Now, solve the multiplication 6(1) which is equal to 6:
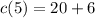
And finally, add 20 and 6:
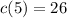
The cost of an ad with 5 lines is $26
Answer: $26