We have to calculate the volume V of the washer.
This can be calculated as the product of the base B and the height H, and B and H are defined in function of x, so we will have a volume V that will be a function of x too.
We can calculate this as:
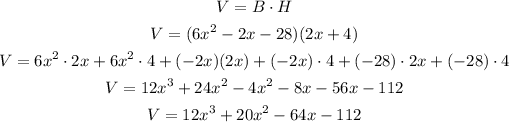
We have applied the distributive property and group the similar terms together.
The volume is 12x^3+20x^64x-112.