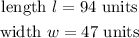Answer:
The value of the length and width is;
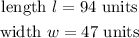
Step-by-step explanation:
Let l and w represent the length and width of the rectangle.
Given that;
The length of a rectangle is twice the width
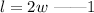
the perimeter is 282.
the formula for perimeter of a rectangle is;
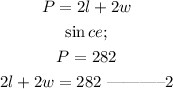
Let us substitute equation 1 to 2;
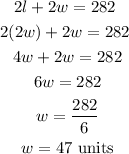
We can now substitute the value of w into equation 1 to get the length l;
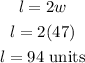
Therefore, the value of the length and width is;