Question

In ∆VWX, w=680 cm, < X =80° and

Answer 1

1) We know that the sum of the interior angles within a triangle is 180º

So we can state that :

∠X = 80º , ∠V=32º and ∠W = 180º-(80+32), ∠W=68º

2) The area of a triangle can be found by the Heron formula, but before that, we need to find out the other legs. Let's sketch this and use the Law of Sines:

The Law of Sines:

`\begin{gathered} (v)/(\sin(V))=(w)/(\sin(W))=(x)/(\sin(X)) \\ (v)/(\sin(32))=(680)/(\sin(68)) \\ 680\text{ sin(32) = vsin(68)} \\ \frac{680\text{ }\sin(32_{}}{\sin(68)}=v \\ v\text{ =}388.65 \\ \\ \end{gathered}`

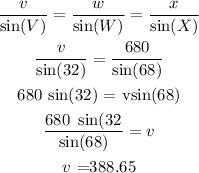
Now let's proceed to find the length of side x:

`\begin{gathered} (w)/(\sin(W))=(x)/(\sin(X)) \\ (680)/(\sin(68))=(x)/(\sin (80)) \\ x\sin (68)=680\cdot\sin (80) \\ x=(680\cdot\sin (80))/(\sin (68)) \\ x\approx722.26 \end{gathered}`

Now we can add the three sides and find out the Perimeter:

2p: 722.26 +388.65 +680

2p=1790.91

And the semi perimeter is p =2p/2, p =895.455.

2.2) Finally we can find out the area using the Heron Formula:

`\begin{gathered} A=\sqrt[]{p(p-v)(p-w)(p-x)} \\ A=\sqrt[]{895.455(895.455-388.65)(895.455-722.455)(895.455-680)} \\ A=130059.9757\approx130060 \end{gathered}`

3) Hence, the area is 130,060 cm²