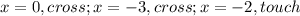Solution:
Given:
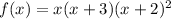
To get the zeros, the zeros exist when f(x) = 0
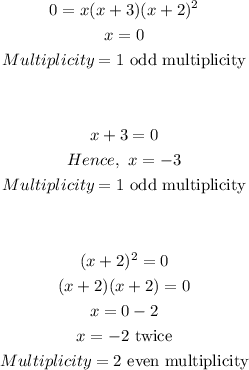
To get the behavior of the graph, the rule below applies;
The graph of a polynomial function will touch the x-axis at zeros with even multiplicities. The graph will cross the x-axis at zeros with odd multiplicities.
The graph of the function showing the x-intercepts and the behavior of the zeros is shown;
Therefore, in conclusion: