Question

Birth weights at a local hospital have a Normal distribution with a mean of 110 oz. and a standard deviation of 15 oz.a) Find the proportion of infants with birth weights above 125 oz. Explain.b) Find the proportion of infants with birth weights between 125 oz. and 140 oz. Explain

Answer 1

a)

Since the weights follow a normal distribution this mean we can use it to find the proportions. In this case the proportion of birth wights above 125 oz is the same as finding the probability:

`P(X>125)`

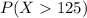
To determine the probability we need to use the standard normal distribution, defined by the z-score:

`z=(x-\mu)/(\sigma)`

where x is the value we are looking for, mu is the mean and sigma is the standard deviation.

Then the probability stated above takes the form:

`P(X>125)=P(Z>(125-110)/(15))=P(Z>1)`

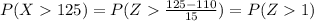
Now, looking at a standard normal distribution table we have:

`P(X>125)=P(Z>1)=0.1587`

Therefore we conclude that 15.87% of the birth weights is above 125 oz.

b)

In this case we are looking for the probability:

[tex]P(125Using the proabability distribution properties we have that:

[tex]P(125transforming this probabilities to z-scores and looking at a table we have:

[tex]\begin{gathered} P(125Therefore the proportion of weights between 125 and 140 oz. is 13.59%