Question

Angle is in standard position and (-6, 7) is a point on the terminal side of 0. Whatis the exact value of sin 8 in simplest form with a rational denominator?

Answer 1

You are asked to find

`\sin (\theta)=\sin (\theta-90^(\circ))`

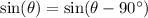
The sin of an angle equals the opposite side divided by the hypotenuse, so the next drawing will help to find the answer:

`\sin (\theta)=\frac{7}{\sqrt[]{6^2+7^2}}=\frac{7}{\sqrt[\square]{85}}`

The hypotenuse is the square root of 6 to the square plus 7 to the square because of the Pythagorean theorem. In order to have a rational denominator:

`\frac{7}{\sqrt[]{85}}=\frac{7\cdot\sqrt[\square]{85}}{85}=\frac{7\cdot\sqrt[]{17}\cdot\sqrt[\square]{5}}{17\cdot5}`

Because