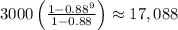Question

I could use some help setting this problem up please.

Answer 1

The formula that would show the total page views that the webpage would have after 9 days would be D. 3, 000 ( ( 1 - 0. 88 )⁹ / ( 1 - 0. 88 ) ) = 17, 088.

How to set up the problem ?

To find the number of total page views on the ninth day, you can use the future value of annuity formula which is:

= Starting views x ( ( 1 + rate ) ⁿ - 1 ) / rate

Starting views = 3, 000

rate = - 12 %

n = 9 days

The number of total views on the ninth day would be:

= 3, 000 x ( ( 1 + ( - 12 %) ⁹ - 1 ) / - 12 %

= 17, 088 people

Simply look at the option that has this number of total views and this would be the correct way to set up the question.

In conclusion, option D is correct.

Answer 2

First, find an expression for the number of page views for the n-th day.

Since each day the number of visitors decreases by 12%, then, the number of page views is 88% of the number of visitors from the previous day. We can find that amount by multiplying 3000 by 0.88.

The n-th day, that amount would have been multiplied by 0.88 n-1 times (the first day, it is multiplied by a factor of 0.88^0, the second day, by 0.88^1, and so on, so the n-th day, the amount of visitors can be found by multiplying by a factor of 0.88^n-1).

Then, the expression for the number of visitors of the n-th day is:

`v_n=3000\cdot0.88^(n-1)`

On the other hand, remember the following formula:

`r^0+r^1+r^2+...+r^(n-1)=(1-r^n)/(1-r)`

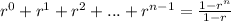
The amount of visitors after nine days can be found as:

`\begin{gathered} v_1+v_2+...+v_9 \\ =3000*0.88^0+3000*0.88^1+...+3000*0.88^8 \\ =3000*(0.88^0+0.88^1+...+0.88^8) \\ =3000*\left((1-0.88^9)/(1-0.88)\right) \\ =17,088.04045... \\ \approx17,088 \end{gathered}`

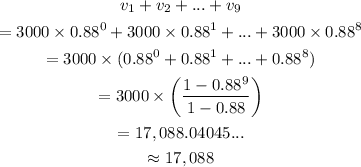
Therefore, the correct choice is:

`3000\left((1-0.88^9)/(1-0.88)\right)\approx17,088`