To draw a scaled copy with a scale factor of 2 of a circle whose radio is r1, draw another circle with a radio r2=2r1, for example, if the radio of your first circle equals 2, the radio of your scaled circle is 2*2=4, like this:
The circumference of a circle is given by the formula:
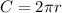
Since the first circle has a radio r1, its circumference is:
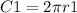
And the second circle has a radio that is two times the radio of the first circle (2r1), its circumference is:
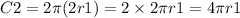
By taking the ratio of the circumference of circle two to the circumference of circle one, we get:
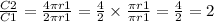
Then, the circumference of the scaled circle is two times the circumference of the circle one.
The area of circle one is given by the formula:
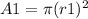
And the area of the scaled circle, whose radio is 2r1, is:
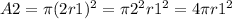
By taking the ratio of A2 to A1, we get:
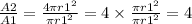
Then, the area of the scaled copy is 4 times the area of the first circle