Question

An object of mass m = 2 kg is initially moving forward when a net force F = 18 N acts on the object in the forward direction. While the force is applied, the object travels a distance x = 6 meters in a time t = 5 seconds.(a) What is the acceleration of the object while the force is applied?(b) How much does the object's kinetic energy increase?(c) How much does the object's momentum increase?(d) How much does the object's speed increase?

Answer 1

(a) 9 m/s

(b) 108 J

(c) 90 kg m/s

(d) 45 m/s

Step-by-step explanation:

Part (a)

By the second law of Newton, the acceleration is equal to

`a=(F)/(m)`

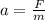
Where F is the net force and m is the mass. So, replacing F = 18 N and m = 2 kg, we get

Then, the acceleration of the object while the force is applied is 9 m/s²

Part (b)

The increase of the kinetic energy can be calculated as

`\Delta K=(1)/(2)m(v^2_f-v^2_i)^{}_{}`

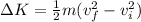
Where m is the mass, vf is the final velocity and vi is the initial velocity. By the kinematic equations, we have the following equality

`v^2_f-v^2_i=2ax`

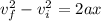
Where a is the acceleration and x is the distance traveled. Replacing this equation on the equation above, we get

`\Delta K=(1)/(2)m(2ax)=m(ax)`

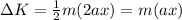
Then, we need to replace m = 2kg, a = 9 m/s² and x = 6 m

Therefore, the kinetic energy increase 108 J.

Part (c)

The change in the momentum can be calculated as

`\Delta p=F\cdot t`

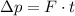
Where F is the force and t is the time. Replacing F = 18N and t = 5 s, we get

`\Delta p=(18\text{ N)(5 s) = 90 kg m/s}`

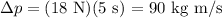
So, the object's momentum increases 90 kg m/s

Part (d)

The change in momentum is also equal to

`\begin{gathered} \Delta p=mv_f-mv_i \\ \Delta p=m(v_f-v_i) \end{gathered}`

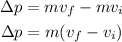
Where (vf - vi) is the object's speed increase. So, solving for (vf - vi), we get

`v_f-v_i=(\Delta p)/(m)`

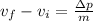
Finally, replace Δp = 90 kg m/s and m = 2 kg, we get

Then, the object's speed increase 45 m/s

So, the answers are:

(a) 9 m/s

(b) 108 J

(c) 90 kg m/s

(d) 45 m/s