Question

suppose that the height (in centimeters) of a candle is a linear function of the amount of time(in hours) it has been burning. after 10 hours of burning, a candle has a height of 17 centimeters. after 23 hours of burning, it's height is 11.8 centimeters. what is the height of the candle after 16 hours.

Answer 1

We want to know the height of a candle after 16 hours.

We know that the height is a linear function of the amount of time (in hours) it has been burning. This means that we can write it as:

`f(x)`

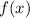
where x represents the number of hours burning.

Also, we have that after 10 hours of burning, the candle has a height of 17 centimeters, which means that we can write it as a point of the function:

And after 23 hours of burning its height is 11.8 centimeters, so we can write the second point of the function will be:

`(23,11.8)`

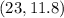
We will find the linear function that describes the height. Using the two points, we will find the slope and the y-intercept.

The slope is given by:

`m=(y_2-y_1)/(x_2-x_1)=(11.8-17)/(23-10)=(-5.2)/(13)=-0.4`

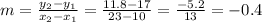
And for the y-intercept, we replace a point on the slope-intercept form, and we clear out the y-intercept.

`\begin{gathered} y=mx+b \\ 17=-0.4(10)+b \\ 17=-4+b \\ 17+4=b \\ 21=b \end{gathered}`

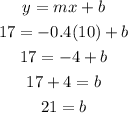
This means that the y-intercept is 21, and the linear function that describes the height is given by:

`y=-0.4x+21`

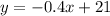
For finding the height of the candle after 16 hours, we replace x by 16, and we obtain:

`\begin{gathered} y=-0.4(16)+21 \\ =-6.4+21 \\ =14.6 \end{gathered}`

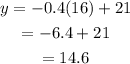
This means that the height of the candle after 16 hours is 14.6 centimeters.