Question

given the function h(x) = x^2 -9x + 26 determine the average rate of change of the function over the interval -10 ≤ x ≤ -2

Answer 1

Given:

The function is,

`h\mleft(x\mright)=x^2-9x+26`

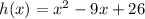
To find:

The average rate of change over the interval

`-10\leq x\leq-2`

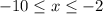
Step-by-step explanation:

Using the formula,

`Average\text{ rate of function}=(f(b)-f(a))/(b-a)`

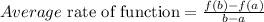
Here,

`\begin{gathered} a=-10 \\ b=-2 \end{gathered}`

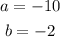
The average rate of the function becomes,

`\begin{gathered} Average\text{ rate of function}=(f(-2)-f(-10))/(-2-(-10)) \\ =((-2)^2-9(-2)+26-((-10)^2-9(-10)+26))/(-2+10) \\ =(4+18+26-(100+90+26))/(8) \\ =(48-216)/(8) \\ =(-168)/(8) \\ =-21 \end{gathered}`

Therefore, the average rate of change of the function is -21.

Final answer:

The average rate of change of the function is -21.