Question

1) Solve. D^3/4=27A) d=36B) d=81Cd=189D)d=1/81

Answer 1

`B)d=81`

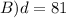
1) The best way to solve this question is to keep in mind that rational exponents can be expressed as roots.

`d^{(3)/(4)}=\sqrt[4]{d^3}`

2) Since this power is equal to 27 we can write out the following:

`\begin{gathered} d^{(3)/(4)}=27 \\ \\ (d^{(3)/(4)})^{(4)/(3)}=27^{(4)/(3)} \\ \\ d=\sqrt[3]{27^4} \\ \\ d=\sqrt[3]{(3^3)^4} \\ \\ d=\sqrt[3]{3^(12)} \\ \\ d=3^{(12)/(3)} \\ \\ d=3^4 \\ \\ d=81 \end{gathered}`

Note that we can use it the property whenever it is more conveninent. That is the answer.