The end of 8 years, Beth will have approximately $3498 in the account if she deposits $2000 at the end of each six-month period at an interest rate of 7%, compounded semiannually.
To calculate the future value of Beth's deposits, you can use the formula for compound interest:
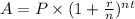
Where:
A is the future value of the investment/deposit.
P is the principal amount deposited at the end of each period, which is $2000 in this case.
r is the annual interest rate, which is 7% or 0.07 in decimal form.
n is the number of times the interest is compounded per year, which is semiannually (twice a year).
t is the number of years.
Given that Beth deposits $2000 at the end of each six-month period (semiannually) for 8 years at an interest rate of 7% compounded semiannually, let's calculate the future value:
First, calculate the number of compounding periods:
n=2×number of years=2×8=16 compounding periods
Now, substitute these values into the formula:
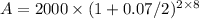


Let's calculate A:
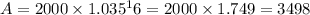
Therefore, at the end of 8 years, Beth will have approximately $3498 in the account if she deposits $2000 at the end of each six-month period at an interest rate of 7%, compounded semiannually.