Question

Graph. Fill in blanks. And include a table of the points

Answer 1

In order to create the table of points, let's choose some values for x and calculate the corresponding value of y:

`\begin{gathered} x=(1)/(2)\colon \\ \log _{(1)/(2)}(1)/(2)+3=1+3=4 \\ \\ x=1\colon \\ \log _{(1)/(2)}1+3=0+3=3 \\ \\ x=2\colon \\ \log _{(1)/(2)}2+3=-1+3=2 \\ \\ x=4\colon \\ \log _{(1)/(2)}4+3=-2+3=1 \end{gathered}`

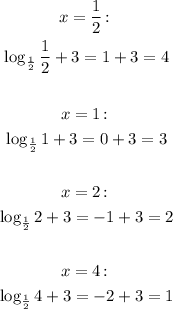
So we have the points (1/2, 4), (1, 3), (2, 2), (4, 1).

Graphing these points and the corresponding curve, we have:

The x-intercept is at x = 8.

As x tends to 0, f(x) tends to infinity.

As x tends to infinity, f(x) tends to minus infinity.

The asymptote is a vertical line at x = 0.