Hello there. To solve this question, we'll have to remember some properties about ratios.
If a car can drive 450 miles on a tank of 30 gallons, we have to determine how far can it drive on 40 gallons.
Assuming these values varies directly, then we have that
Let x be the distance that can be travelled with 40 gallons, such that
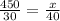
Simplify the fraction on the LHS by a factor of 30

Multiply both sides of the equation by a factor of 40
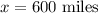
Now, we have to find how many gallons are needed to drive 960 miles.
Using the same values we found, say y is the number of gallons needed to drive 960 miles, such that

Simplifying the fraction
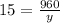
Cross multiply the values, such that
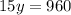
Divide both sides of the equation by a factor of 15
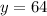
So the car needs 64 gallons in order to drive 960 miles.