Question

Need help finding the lengths of the sides of the triangle

Answer 1

For the triangle is right, the Pythagorean theorem holds; namely,

`(x+5)^2=x^2+(x+4)^2`

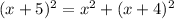
Now, we need to remember the formula for the square of a sum:

`(a+b)^2=a^2+2ab+b^2`

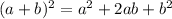
Then, the first equality becomes

`\begin{gathered} x^2+10x+25=x^2+x^2+8x+16,\text{ above identity} \\ 10x+25=x^2+8x+16, \\ x^2-2x-9=0, \end{gathered}`

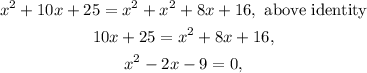
Now, we need to calculate the roots of the polynomial on the left. Let's use the general formula:

`\begin{gathered} x=\frac{-(-2)\pm\sqrt[]{(-2)^2-4(1)(-9)}}{2}, \\ x=\frac{2\pm\sqrt[]{4+36}}{2}, \\ x=(2)/(2)\pm\frac{\sqrt[]{40}}{2}, \\ x_1=1+\sqrt[]{10},x_2=1-\sqrt[]{10} \end{gathered}`

Note that x_2 is negative. It doesn't work for negative lengths makes no sense. Then,

`x=1+\sqrt[]{10}\approx4.2`
`x+4=(1+\sqrt[]{10})+4\approx8.2`
`x+5=(1+\sqrt[]{10})+5\approx9.2`