Solution
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the theorem for exterior angles
The sum of exterior angles of a regular polygon is 360 degrees. This implies that "A regular polygon with n number of sides has the sum of all the exterior angles to be 360 degrees.
From the theorem above,
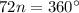
STEP 2: find the number of sides
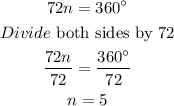
Hence, the regular polygon has 5 sides