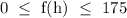Question

6. Tara has an after school job at the local stationary store. She makes $8.75 an hour. Tara never works more than 20 hours in a week. Write an equation that models this scenario where h is the number of hours and f(h) is the amount of money Tara makes in a week. a. b. What is the domain of the function? (Represent your response in inequality notation.)" C. What is the range of the function? (Represent your response in inequality notation.)

Answer 1

`\begin{gathered} a)\text{ f(h) = 8.75h} \\ b)\text{ 0}\leq\text{ h }\leq\text{ 20 or h }\leq\text{ 20} \\ c)\text{ 0}\leq\text{ f(h) }\leq\text{ 175 or f(h) }\leq\text{ 175} \end{gathered}`

a) We want to write an equation

From the question, she works and earn $8.75 per hour

An equation representing this, with f(h) being the amount earned will be;

`f(h)\text{ = 8.75h}`

b) Here, we want to get the domain of the function

When we talk of the domain, we are simply referring to the possible number of hours worked. From the question, we are told that this cannot be more than 20 hours

Mathematically, we can have this as;

`0\text{ }\leq\text{ h }\leq\text{ 20}`

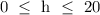
What this mean is that the number of possible hours to work per week is between 0 and 20

c) We want to get the range of the function

The range represents the possible amount of money she can earn

From the question, we are told that she work more than 20 hours at a rate of $8.75 per hour

Thus, the highest possible amount to be earned is 20(8.75) = $175

So, the range of the function will be;

`0\text{ }\leq\text{ f(h) }\leq\text{ 175}`