Question

What is the average velocity of atoms in 1.00 mol of neon (a monatomic gas) at 288K?Use the equation 1/2mv^2 =3/2nRTFor m use 0.01000 kg. Remember that R-8.31 J/(mol.K).A. 847 m/sB. 718,000 m/sC. 8.47 m/sD. 71.8 m/s

Answer 1

the Given

*The number of mol of neon is n = 1 mol.

*The temperature of the neon gas is T = 288 K.

*The mass of the neon gas is m = 0.01 kg.

*The gas constant R is R = 8.31 J/(mol.K).

To find: The average velocity of atoms of neon (v).

According to the given equation,

`(1)/(2)mv^2=(3)/(2)nRT`

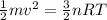
Substitute the known values.

`\begin{gathered} (1)/(2)*0.01\text{ kg}* v^2=(3)/(2)*1\text{ mol}*8.31\text{ J/mol.K}*288\text{ K} \\ 5*10^(-3)\text{ kg}* v^2=(3)/(2)*2393.28\text{ J} \\ 5*10^(-3)\text{ kg}* v^2=3589.92\text{ J}*\frac{1(kg.m^2)/(s^2)}{1\text{ J}} \\ v^2=\frac{3589.92\text{ }(kg.m^2)/(s^2)}{5*10^(-3)\text{ kg}} \\ v^2=717984(m^2)/(s^2) \\ v=\sqrt[]{717984(m^2)/(s^2)} \\ v=847.33\text{ m/s} \\ v\cong847\text{ m/s} \end{gathered}`

The average velocity of atoms of neon is 847.33 m/s. Thus, option (A) is the correct answer.