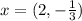The given quadratic equation is
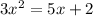
First of all, let us re-write the equation in standard form.
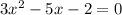
Recall that the standard form of a quadratic equation is given by

Comparing the standard form with the given equation we see that,
a = 3
b = -5
c = -2
Now we can solve using the quadratic formula.
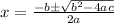
Let us substitute the values of the coefficients a, b, c
![\begin{gathered} x=\frac{-(-5)\pm\sqrt[]{(-5)^2-4(3)(-2)}}{2(3)} \\ x=\frac{5\pm\sqrt[]{25^{}-(-24)}}{6}=\frac{5\pm\sqrt[]{25^{}+24}}{6}=\frac{5\pm\sqrt[]{49}}{6}=(5\pm7)/(6) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/fdy5v9z8slrmgeu5pergemufee01zg217n.png)
So, the two possible solutions of the quadratic equation are
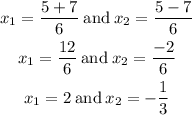
Therefore, the solution of the given quadratic equation is