Question

Rendering math...The difference of two numbers is 5. The sum of three times the larger number and twicethe smaller number is 30. What is the smaller number?A1B2C3D4E5

Answer 1

We have to transform each sentence into an algebraic expression.

"The difference between two numbers is 5" can be expressed as

`x-y=5`

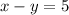
"The sum of three times the larger number and twice the smaller number is 30" can be expressed as

`3x+2y=30`

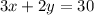
Where x is the larger number, and y is the smaller number.

We form a system of equations with these two

`\left\{ \begin{aligned}x-y=5 \\ 3x+2y=30\end{aligned}\right.`

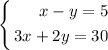
We can multiply the first equation by 2 and sum them to find the first variable

`\begin{gathered} \left\{ \begin{aligned}2x-2y=10 \\ 3x+2y=30\end{aligned}\right.\rightarrow5x=40 \\ \end{gathered}`

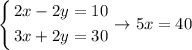
Then, we divide the equation by 5

`\begin{gathered} (5x)/(5)=(40)/(5) \\ x=8 \end{gathered}`

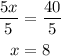
The larger number is 8.

Now, we find the smaller numbers using the first equation

`\begin{gathered} x-y=5 \\ 8-y=5 \\ -y=5-8 \\ -y=-3 \\ y=3 \end{gathered}`

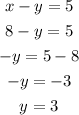
The smaller number is 3.

Therefore, the right answer is C.