Question

Given the function f(x)=x^2-4x+0, determine the average rate of change of the function over the interval −3≤x≤4.

Answer 1

STEP - BY - STEP EXPLANATION

What to find?

The average rate of change of the given function over the given interval.

Given:

`\begin{gathered} f(x)=x^2-4x+0 \\ \\ -3\leq x\leq4 \end{gathered}`

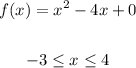
Step 1

Determine f(-3).

Substitute x=-3 into the function and simplify.

`\begin{gathered} f(-3)=(-3)^2-4(-3)+0 \\ \\ =9+12 \\ \\ =21 \end{gathered}`

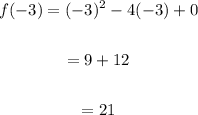
Step 2

Calculate f(4)

Substitute x=4 into the function and simplify.

`\begin{gathered} f(4)=(4)^2-4(4)+0 \\ \\ =16-16+0 \\ \\ =0 \end{gathered}`

Step 3

State the formula for average rate of change.

`Average\text{ rate of change=}(f(x_2)-f(x_1))/(x_2-x_1)`

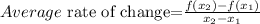
Let x₁