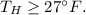We define the notation:
• T_H = high temperature,
,
• T_L = low temperature.
From the statement of the problem, we know that:
• the difference between the temperatures was at least 35°F:

• the low temperature was:

Replacing the value of the low temperature in the inequality above, we find that:
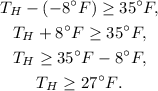
Answer
We find that the high temperature was at least 27°F: