Question

Find the measure of PR¯¯¯¯¯¯¯¯.secant-tangent 19A. 25B. 18C. 22D. 19

Answer 1

We have the following drawing showing a case of two secants in a circle:

And we need to find the value of PR, that is, the measure of the secant PR.

1. To find that value, we need to remember the secant-secant formula for circles:

That is, the product of the measure of one whole secant and its external part is equal to the product of the measure of the other whole secant and its corresponding part.

2. Then, we have that:

`\begin{gathered} \text{ Whole secant \lparen left side\rparen = FR=FS+SR=7+9=16} \\ \\ \text{ External part of the secant \lparen left side\rparen = SR = 9} \end{gathered}`

And the measure of the other secant is:

`\begin{gathered} \text{ Whole secant \lparen right side\rparen = PR=PQ+QR = 5x + 8} \\ \\ \text{ External part of the secant \lparen right side\rparen = QR = 8} \end{gathered}`

3. Now, we can apply the rule as follows:

`16(9)=(5x+8)8`

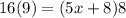
4. Now, we have to expand the equation, and solve it for x as follows:

`\begin{gathered} 144=5x(8)+8(8)=40x+64 \\ \\ 144=40x+64 \\ \\ \end{gathered}`

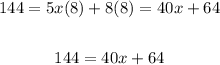
5. Subtracting 64 from both sides of the equation, we have:

`\begin{gathered} 144-64=40x+64-64 \\ \\ 80=40x \end{gathered}`

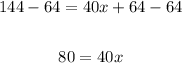
6. Dividing both sides of the equation by 40, we have:

`\begin{gathered} (80)/(40)=(40)/(40)x \\ \\ 2=x \\ \\ x=2 \end{gathered}`

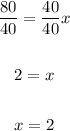
Then, since we have that PR = 5x + 8, we have to substitute the value of x into this equation:

`\begin{gathered} PR=5(2)+8=10+8=18 \\ \\ PR=18 \end{gathered}`

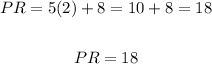
Therefore, in summary, the measure for PR is 18 (PR = 18) (option B.)