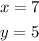Answer:
the solution to the system of equation is;
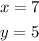
Exp
Given the system of equation;
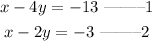
We want to solve by elimination.
subtract equation 1 from equation 2;
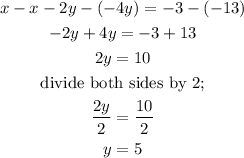
If y=5, then the value of x can be derived using equation 2 as;
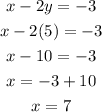
Therefore, the solution to the system of equation is;