Answer:
The volume of the trapezoidal ditch is 486000 in³. The volume of the half-cylinder ditch is 457812 in³. Therefore, the trapezoidal ditch holds a greater volume of water
Step-by-step explanation:
Given:
Two flood control ditches; one is a trapezoidal ditch and the other a half cylinder
To find:
the volume of the two ditches and compare which has a greater volume of water
To determine the shape with higher volume, we need to find the volume of each of the ditches
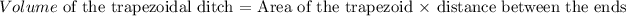

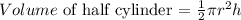
![\begin{gathered} let\text{ }\pi\text{ = 3.14, r = 90 in, } \\ \text{h = 3ft = 36 in} \\ Volume\text{ of the half cylinder = }(1)/(2)*3.14*90^2*36 \\ Volume\text{ of the half cylinder = 457812 in}^3 \\ \\ NB:\text{ the value of the volume for the half cylinder will vary depending on the value of \pi used} \end{gathered}]()
The volume of the trapezoidal ditch is greater than the volume of the half-cylinder
The volume of the trapezoidal ditch is 486000 in³. The volume of the half-cylinder ditch is 457812 in³. Therefore, the trapezoidal ditch holds a greater volume of water