Question

2. Which of the following equations are perpendicular to 2y = -3x + 1 1. Which of the following have the same domain and range? I. y = 2x - 1 II. y = -x +2 X = 2 1. y = -1 II. III. у -2x + 3y = -5 2x + 3y = 2 (A) I and III only (B) I and II only (C) II and III only (D) I, II and III (A) I only (B) I and II only (C) II and III only (D) I and Ill only

Answer 1

If we have a line defined by the equation

`y=mx+b`

Then the equation of a line perpendicular to the above line is

`y=-(1)/(m)x+c`

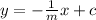
In our case, we are given the equation

`2y=-3x+1`

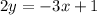
Dividing both sides by 2 gives us the slope-intercept form

`y=-(3)/(2)x+1`

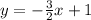
Now, an equation perpendicular to the above will be

`y=(2)/(3)x+c`

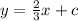
where c is any constant.

Now we need to look at the choices given and see which ones have the form given above, and to do that we go through each other choices one by one.

(I) y = 2 /3 x -1

This has the slope 2/3 meaning it is perpendicular to the line given; therefore, this is a correct choice.

(II) -2x+ 3y = -5

Converting the above to the slope-intercept form gives

`y=(2)/(3)x-(5)/(3)`

This has a slope of 2/3, meaning this line is perpendicular to the line given; therefore, this also is a correct choice.

(III) 2x + 3y = 2

Converting the above to the slope-intercept form gives

`y=-(2)/(3)x+(2)/(3)`

The slope of the above equation is not 2/3 and so the line described by this equation is not perpendicular to the line given; therefore, this is not a correct choice.

Hence, only choices (I) and (II) stand correct and therefore, option B is correct.