Question

Suppose that the function f is defined, for all real numbers, as follows.3x+1 if x<-2f(x)=x-3 if x>-2Graph the function f. Then determine whether or not the function is contin

Answer 1

Given function is,

`\begin{gathered} f(x)=3x+1\text{ if }x<-2 \\ f(x)=x-3\text{ if }x\ge-2 \end{gathered}`

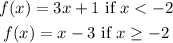
The function 3x+1 and x-3 are continuous function.

To ensure the function f(x) is continuous, we need to show that the function is continuous at the point x=-2.

The function is specified at x = -2,

we get,

`f(-2)=-5`

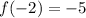
Then we need the limit of the function as x addresses -2 exists.

Consider the left hand limit, we get

`\lim_(x\to-2^-)f(x)=\lim_(x\to-2^-)3x+1=3(-2)+1=-5`

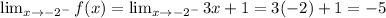
Consider right hand limit, we get

`\lim_(x\to-2^+)f(x)=\lim_(x\to-2^+)x-2=-3-2=-5`

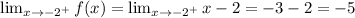
we get that,

`\lim_(x\to-2^-)f(x)=\lim_(x\to-2^+)f(x)`

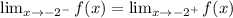
Left hand limit= Right hand limit

The limit of the function as x addresses -2 exists.

Next to check the limit of the function as x addressing -2 is equal to the function value at x = -2

`\begin{gathered} \lim_(x\to-2)f(x)=-5 \\ \\ f(-2)=-5 \\ \text{ we get,} \\ \lim_(x\to-2)f(x)=f(-2) \end{gathered}`

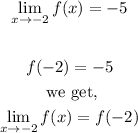
Therefore we get, The limit of the function as x addressing -2 is equal to the function value at x = -2.

Hence the function is continuous at x=-2.

Therefore, the function f(x) is continuous function.

The graph of the function is,