Given
The product of three consecutive odd numbers is 2145.
To find the numbers.
Step-by-step explanation:
Let be an odd number.
That implies, the three consecutive odd numbers are,
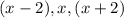
Since their product is 2145.
Then,
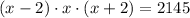
Since the prime factorization of 2145 is,
That implies,
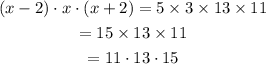
Hence, the three consecutive odd numbers is 11, 13, 15.
And,
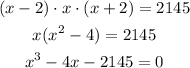
Therefore, the polynomial is,
