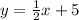Question

Which equation represents the line that contains the points (2, 6) and (–2, 4)?y = One-half x + 7y = One-half x + 5y = Five-halves x + 1y = Five-halves x + 11

Answer 1

y = (1/2)x + 5

Explanation

Equation of a line in slope-intercept form

`y=mx+b`

where m is the slope and (0, b) is the y-intercept

The slope of the line that passes through the points (x₁, y₁) and (x₂, y₂) is calculated as follows:

`m=(y_2-y_1)/(x_2-x_1)`

In this case, the line passes through the points (2, 6) and (-2, 4), then its slope is:

`\begin{gathered} m=(4-6)/(-2-2)\frac{}{} \\ m=(-2)/(-4) \\ m=(1)/(2) \end{gathered}`

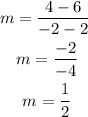
Substituting with the point (2, 6), that is, x = 2 and y = 6, and m = 1/2 into the general equation, and solving for b:

`\begin{gathered} 6=(1)/(2)\cdot2+b \\ 6=1+b \\ 6-1=1+b-1 \\ 5=b \end{gathered}`

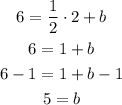
Finally, substituting m = 1/2 and b = 5 into the general equation, the equation of this line is:

`y=(1)/(2)x+5`