Let the variable "x" represent the number of advanced tickets sold and variable "y" the amount of same-day tickets sold.
For a function there were a total of 60 tickets sold, between the advanced and the same- day tickets. You can express the total number of tickets sold as an equation with two unknowns:
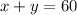
Each "advanced" ticket costs $35, if x advanced tickets were sold, the total amount will be 35x
Each "same-day" ticket costs $40, for the y tickets sold, the total amunt will be 40y
If $2200 were collected in total, you can express the total amount earned as an equation with two unknowns:
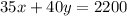
With this we have an equation system determined, now we can proceed to solve it:
Step 1, write the first equation in terms of one of the variables.
I'll do it for x:
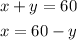
Stept 2, replace the expression of step 1 in the second equation:
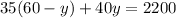
Now you can solve for y. First solve the term in parentheses by applying the distributive propperty of multiplications:
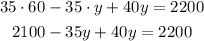
Next pass the number to the left side and add both y-related terms:
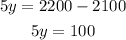
Finally divide both sides by 5 to determine the amount of "same-day" tickets sold:
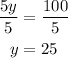
Now that you know the value of y, replace it in the first formula to determine the value of x

So, there were sold 35 tickets in advance and 25 same-day tickets.