Part A. We are given that rock is thrown straight upwards from a bridge with an initial velocity of +35 m/s. To determine the velocity after 2 seconds we will use the following equation of motion for the velocity of a body in free fall:
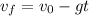
Where:
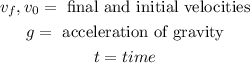
Now, we plug in the values:
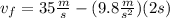
Now, we solve the operations:
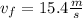
Therefore, the velocity after 2 seconds is 15.4 m/s.
Part B. To determine the displacement we will use the following formula:
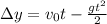
Now, we substitute the values:
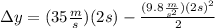
Solving the operations:
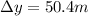
Therefore, the displacement is 50.4 meters.