We will investigate the effect of translation on a given function f ( x ).
Translation is a type of transformation that deals with a given function f ( x ) in such a way that it displaces the entire function in four possible directions: up,down,left and right.
The number of units a function is to be translated in any direction is given by values of some characteristic constant.
The translated function can be expressed in a generalized form:
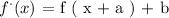
Where,

Each of the characteristic constant of translation ( a and b ) can be used to determine the direction of translation. The guidelines that are used to express ( a and b ) are:

The signs of each constant determine the exact direction of translation.
We are given a function f ( x ) as follows:
![y\text{ = }\sqrt[]{x}](https://img.qammunity.org/2023/formulas/physics/college/ddjg81sxdjpqwx6w53rse6blm3jae6uv8d.png)
We are asked to find the new function such that the original function ( y ) has been translated ( 4 ) units to the left.
Using the above guidelines we can say that we are undergoing only horizontal translation; hence:
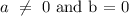
So the general form is reduced down to:
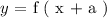
To determine the value and sign of characteristic constant ( a ) we will use the next set of guidelines. All left translations are accompanied by a positive value of ( a ). Hence,
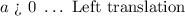
The magnitude of the left translation given is ( 4 units ). Hence, the value of the characteristic constant is:
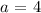
Then the generalized function depiction would be:
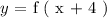
We will substitute whatever is within the parenthesis of the f ( x + 4 ) into the given function ( x ) as follows:
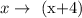
Then the resulting translated function would be expressed as:
![\textcolor{#FF7968}{y}\text{\textcolor{#FF7968}{ = }}\textcolor{#FF7968}{\sqrt[]{(x+4)}\ldots}\text{\textcolor{#FF7968}{ Answer ( Option B )}}](https://img.qammunity.org/2023/formulas/mathematics/college/80l7cpwsuzceue24ykm8a84bl8qvqmyci2.png)