Answer:
Let s be the length of the shortest side, then the length of the longest side is s+7cm, and the lengths of the remaining sides are both equal to 3s.
Now, recall that the perimeter of a trapezoid is the sum of the lengths of its sides, therefore we can set the following equation:
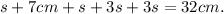
Adding like terms in the above equation we get:
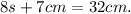
Subtracting 7cm from the above equation we get:
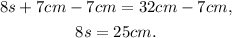
Dividing the above equation by 8 we get:
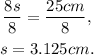
Therefore the length of the shortest side is 3.125cm.
The length of the longest side is
![3.125\operatorname{cm}+7\operatorname{cm}=10.125\operatorname{cm}\text{.}]()
The lengths of the remaining two sides are:
![3*3.125\operatorname{cm}=9.375\operatorname{cm}\text{.}]()