Question

Ali works as a Quality Manager and as part his job he has to place products intothree different categories: Red, Amber and Green. Ali knows the probability ofplacing product X in Green category is 0.67 and that of placing product X in Ambercategory is 73% smaller than the probability of Green. Calculate the probability ofplacing product X in Red category and state any assumption(s) you have made.

Answer 1

From the present question, we know that a specific product X will be placed in one of the three listed categories. Because it must be placed in one of the three, the sum of the probabilities of each group have to be equal to 100%. From this, we can write:

`P_R+P_A+P_G=1`

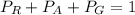
Where the P's stand for the probability of each group. It was given that the probability of X to be placed in group Green is 0.67, and the Ambar is 0.73 smaller than the probability for Green. From this, we can write the following relation.

`\begin{gathered} P_A=P_G-0.73P_G \\ \\ P_A=0.67-0.73*0.67=0.1809 \end{gathered}`

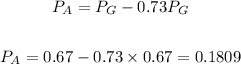
From this, we can rewrite the first relation with the values as follows:

`\begin{gathered} P_R+0.1809+0.67=1 \\ P_R=1-0.67-0.1809=0.1491 \end{gathered}`

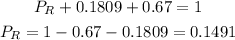
From the present solution, we conclude that the probability if the product X to be placed in category Red is equal to 0.1491, or 14.91%.