Question

An elevator has a placard stating that the maximum capacity is 1750 lb—10 passengers. So, 10 adult male passengers can have a mean weight of up to 1750/10=175 pounds. If the elevator is loaded with 10 adult male passengers, find the probability that it is overloaded because they have a mean weight greater than 175 lb. (Assume that weights of males are normally distributed with a mean of 180 lb and a standard deviation of 25 lb.) Does this elevator appear to be safe?

Answer 1

- The Z-score we need to find is the value of weights greater than 175.

- The Z-score is:

`\begin{gathered} Z=(X-\mu)/((\sigma)/(√(n))) \\ \\ \text{ We are looking for }X>175 \\ \\ Z=(175-180)/((25)/(√(10))) \\ \\ Z=-0.632455... \end{gathered}`

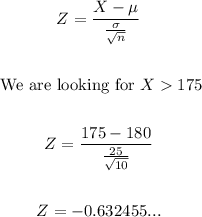
- Thus, we can find the probability that the weights of the males is greater than 175 using a z-score calculator.

Final Answer

The probability is 0.7365