The given expression is
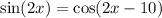
To find the correct value, we just have to evaluate each option.
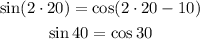
This is not true, so x = 20 is not the solution.
x = 21.
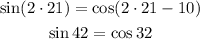
x = 24
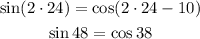
x = 25.
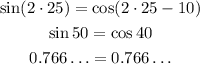
As you can observe, the last option satisfies the equation.
Therefore, option 4 is the answer.