1 Answer

Fesler · Answer 1 · 2023-05-17T09:04:48+0000

The given expression is

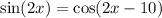
$\sin (2x)=\cos (2x-10)$

To find the correct value, we just have to evaluate each option.

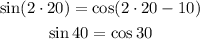
$\begin{gathered} \sin (2\cdot20)=\cos (2\cdot20-10) \\ \sin 40=\cos 30 \end{gathered}$

This is not true, so x = 20 is not the solution.

x = 21.

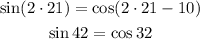
$\begin{gathered} \sin (2\cdot21)=\cos (2\cdot21-10) \\ \sin 42=\cos 32 \end{gathered}$

x = 24

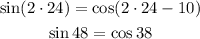
$\begin{gathered} \sin (2\cdot24)=\cos (2\cdot24-10) \\ \sin 48=\cos 38 \end{gathered}$

x = 25.

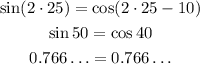
$\begin{gathered} \sin (2\cdot25)=\cos (2\cdot25-10) \\ \sin 50=\cos 40 \\ 0.766\ldots=0.766\ldots \end{gathered}$

As you can observe, the last option satisfies the equation.

Please log in or register to add a comment.