1 Answer

Estan · Answer 1 · 2023-07-15T09:05:38+0000

We are given that the tension of a ligament is proportional to its extension. Therefore, we have from Hook's law:

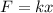
Where:

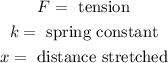
$\begin{gathered} F=\text{ tension} \\ k=\text{ spring constant} \\ x=\text{ distance stretched} \end{gathered}$

Now, we are asked to determine the tension of a string given that is stretched a distance of 0.780 cm:

$F=(150\frac{N}{\operatorname{mm}})(0.78\operatorname{cm})$

Now, we need to convert the centimeters into millimeters. To do that we will use the following conversion factor:

$1\operatorname{cm}=10\operatorname{mm}$

Now, we multiply by the conversion factor:

$F=(150\frac{N}{\operatorname{mm}})(0.78\operatorname{cm}*\frac{10\operatorname{mm}}{1\operatorname{cm}})$

Now, we solve the operations:

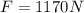
Now, we convert the "N" into "kN" using the following conversion factor:

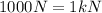
Multiplying by the conversion factor we get:

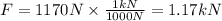
Therefore, the tension is 1.17 kN.

Now, the elastic energy is given by:

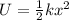
Substituting the values we get:

$U=(1)/(2)(150\frac{N}{\operatorname{mm}})(0.78\operatorname{cm}*\frac{1\operatorname{cm}}{10\operatorname{mm}})^2$

Solving the operations:

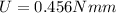
Now, to covert the energy into Joules we need to covert the "mm" into "m". To do that we use the following conversion factor:

$1000\operatorname{mm}=1m$

Multiplying by the conversion factor:

$U=0.456\text{Nmm}*\frac{1m}{1000\operatorname{mm}}$

Solving the operations:

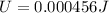
Therefore, the elastic energy is 0.000456 Joules.

Please log in or register to add a comment.