Question

What is the magnitude of the acceleration that the engine must produce

Answer 1

`\begin{equation*} 111.6\text{ }m\/s^2 \end{equation*}`

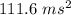
Step-by-step explanation

To find the magnitude of the acceleration, find the components of the acceleration on the x and y-axis.

In the x-direction, we can find the acceleration using the formula:

`x=x_0+v_0t+(1)/(2)a_xt^2`

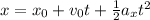
where t = time taken

x = distance traveled in the x-direction

a = acceleration in the x-direction

v0 = initial velocity in the x-direction

x0 = 0 m

Hence, the acceleration in the x-direction is:

`\begin{gathered} 19500\cos32=0+(1810\cos20)(9.20)+(1)/(2)*a_x*(9.20)^2 \\ 16536.94=15647.76+42.32a_x \\ 42.32a_x=16536.94-15647.76=889.18 \\ a_x=(889.18)/(42.32) \\ a_x=21.01\text{ }m\/s^2 \end{gathered}`

In the y-direction, we can find the acceleration using the formula:

`y=y_0+v_0t+(1)/(2)a_yt^2`

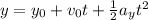
where y = distance traveled in the y-direction

y0 = 0 m

Hence, the acceleration in the y-direction is:

`\begin{gathered} 19500\sin32=0+(1810\sin20)(9.20)+(1)/(2)a_y*9.20^2 \\ 10333.43=5695.32+42.32a_y \\ 42.32a_y=10333.43-5695.32=4638.11 \\ a_y=(4638.11)/(42.32) \\ a_y=109.6\text{ }m\/s^2 \end{gathered}`

The magnitude of the acceleration is given by:

`a=√(a_x^2+a_y^2)`

Therefore, the magnitude of the acceleration is:

`\begin{gathered} a=√(21.01^2+109.6^2) \\ a=√(441.4201+12012.16)=√(12453.5801) \\ a=111.6\text{ }m\/s^2 \end{gathered}`

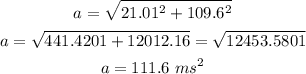
That is the answer.