1 Answer

Ask a Question

Rohit Kaushik · Answer 1 · 2023-03-29T16:04:40+0000

The standard deviation for a sample is given by:

$s=\sqrt[]{\frac{\sum^n_(i\mathop=1)(x_i-\bar{x})}{n-1}}$

where n is the sample size, xi are the values of the data and x bar is the mean of the data.

Let's find the mean first:

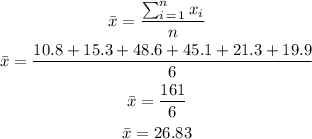
$\begin{gathered} \bar{x}=(\sum ^n_(i\mathop=1)x_i)/(n) \\ \bar{x}=(10.8+15.3+48.6+45.1+21.3+19.9)/(6) \\ \bar{x}=(161)/(6) \\ \bar{x}=26.83 \end{gathered}$

Now that we have the mean we can calculate the standard deviation:

$\begin{gathered} s=\sqrt[]{\frac{\sum^n_{i\mathop{=}1}(x_i-\bar{x})}{n-1}} \\ =\sqrt[]{((10.8-26.83)^2+(15.3-26.83)^2+(48.6-26.83)^2+(45.1-26.83)^2+(21.3-26.83)^2+(19.9-26.83)^2)/(6-1)} \\ =\sqrt[]{(1276.2334)/(5)} \\ =15.98 \end{gathered}$

Therefore, the standard deviation of the data is 15.98

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions