Question

Calculas, prove that there is no tangent to the line

Answer 1

The given equation is,

`p(x)=3x^2+6x\text{ ---(1)}`

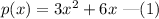
Differentiate the above equation.

`\begin{gathered} (dp(x))/(dx)=3*2x+6 \\ (dp(x))/(dx)=6x+6\text{ ---(2)} \end{gathered}`

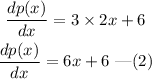
dp(x)/dx is the slope of the tangent to curve p(x).

The given point is (x, y)=(-1, 5).

Take x=-1 and put it in equation (1).

`\begin{gathered} y=p(x)=3*(-1)^2+6*(-1) \\ =3-6 \\ =-3 \end{gathered}`

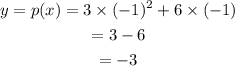
So, the y coordinate is not 5. Hence, there is no tangent to p(x) that passes through point (-1, 5)