Question

Determine all values of x that make the expression true. work in the space provided.

Answer 1

The equation is given as shown below:

`(2)/(x-3)=(x+4)/(x)`

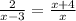
Step 1

Apply fraction cross multiply, defined as:

`\begin{gathered} If \\ (a)/(b)=(c)/(d) \\ \text{then} \\ a\cdot d=b\cdot c \end{gathered}`

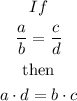
Thus, we have:

`\Rightarrow2x=(x-3)(x+4)`

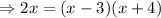
Step 2

Expand the right-hand side of the equation using the FOIL method given to be:

`(a+b)(c+d)=ac+ad+bc+bd`

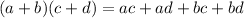
Thus, we have:

`(x-3)(x+4)=x^2+4x-3x-12=x^2+x-12`

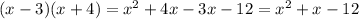
Therefore, the expression becomes:

`2x=x^2+x-12`

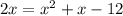
Step 3

Write out the equation in the standard form of a quadratic equation given to be:

`ax^2+bx+c=0`

Hence, we have:

`\begin{gathered} x^2+x-2x-12=0 \\ x^2-x-12=0 \end{gathered}`

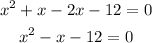
Step 4

Solve using the quadratic formula given to be:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Given

`\begin{gathered} a=1 \\ b=-1 \\ c=-12 \end{gathered}`

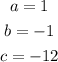
Hence, we have:

`\begin{gathered} x=\frac{-(-1)\pm\sqrt[]{(-1)^2-(4*1*\lbrack-12\rbrack)}}{2*1}=\frac{1\pm\sqrt[]{1+48}}{2}=\frac{1\pm\sqrt[]{49}}{2} \\ x=(1\pm7)/(2) \end{gathered}`

Therefore, the values of x can be:

`\begin{gathered} x=(1+7)/(2)=(8)/(2)=4 \\ or \\ x=(1-7)/(2)=(-6)/(2)=-3 \end{gathered}`

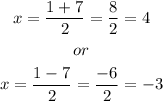
Therefore, the possible solutions to the equation are:

`x=4,x=-3`

Step 5

Check for undefined points. This we can do by equating the denominator of the equation to zero.

Therefore, the undefined points are at:

`\begin{gathered} x-3=0 \\ \therefore \\ x=3 \end{gathered}`

or

`x=0`

ANSWER

Combining the solution and the undefined points, given that none of the solutions are at the undefined points, the solution to the expression is given to be:

`x=4,x=-3`